Concepts of binary, octal, and hexadecimal number systems in digital logic

Understanding the fundamentals of number systems is paramount to comprehending intricate circuits and complex algorithms. Many number systems exist, out of which binary, octal, and hexadecimal take the first place. These systems have an integral role while representing and manipulating data within digital circuits, computers, and microcontrollers. Delving into the concepts of binary, octal, and hexadecimal reveals their inherent efficiency when working with digital data.

To ease the intricate concepts of digital logic, Manipal University Jaipur presents the Online BCA Programme. This 3-year-long course makes you industry-ready with the guidance of industry leaders. From case studies to acquiring market-relevant skills, you can gain a lot from this course. Join now and get set to tackle the competitive world of computer applications. 

Comprehending the Basics of Number Systems

In any kind of calculation, number systems serve as their foundation. While most of us are acquainted with the decimal system, which uses a base of 10 and digits from 0 to 9, the world of digital logic introduces us to alternative number systems fundamental to computing processes.

When exploring the basics of the number system, it has a set of symbols or digits and a base value.  The number of unique symbols utilised in the system is determined by the base value. For instance, in the decimal system, the base value is 10, and 0 to 9 are the symbols that represent values from zero to nine, respectively.  

Binary, octal, and hexadecimal number systems are usually utilised in digital logic. To understand them in detail, read further.

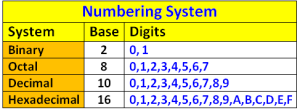
How Does Binary Number System Work?

If you need to name the foundation of the number system in digital computation, it is the binary number system. By leveraging only two symbols, 0 and 1, the binary system represents the principle of binary logic. It is one of the best languages to represent and manipulate digital data. 

The binary number system primarily operates on a base of 2. It signifies that each digit’s value is a power of 2. The digit at the rightmost position has the least significance. On the other hand, the digit on the extreme left is the most significant. For instance, 1010 is the binary number that represents the sum of 24 (16) and 21 (2), which is equal to the decimal value 18. 

One of the prime advantages of the binary number system is its direct correspondence to the binary logic behind it, as used in digital electronics. In binary logic, signals are represented by two states, on and off or true and false. These align perfectly with the binary digits 1 and 0. This alignment allows electronic circuits to perform logical operations, like AND, OR, and NOT, using simple switches called transistors, which can be either on or off.

Unravelling the Octal Number System

The octal number system can be called the bridge that mends the gap between the decimal and binary number systems. It offers a convenient shorthand for representing binary data. It has a base of 8 and digits ranging from 0 to 7. It provides a compact way to express binary values.

This system operates on the principle that each digit will represent a group of three binary digits. These groups are termed bits. By condensing three binary digits into a single octal digit, octal numbers offer a concise representation while maintaining the integrity of the binary information.

Octal has immense utility in computer programming and digital circuit design. When dealing with large binary values, expressing them in octal form simplifies readability and reduces the length of numerical representations.

What Does a Hexadecimal Number System Mean?

Like binary and octal number systems, the hexadecimal number system is another convenient way to represent and manipulate binary data. It has a base of 16 and digits between 0 and 9, plus letters from A to F. This is a farther concise format than the octal number system. 

The hexadecimal number system is valuable when working with binary values of large size. Hexadecimal does not have the problem associated with binary and octal number systems with representations. Both binary and octal representations tend to become lengthy soon, which can be avoided with a hexadecimal system. 

The hexadecimal number system plays a significant role in programming and debugging. Memory dumps and machine code instructions are commonly represented in hexadecimal. This facilitates the analysis and identification of specific patterns or issues within a programme. It also simplifies bitwise operations and binary arithmetic, making it an essential tool for programmers.

Final Words

Having a grip on the binary, octal, and hexadecimal number system concepts is essential for a complete understanding of digital logic.  Each of these systems has distinct properties and applications in the world of computation. By grasping each of these concepts, you can easily manipulate and convert data across various bases. Thus, enabling efficient programming, computation, and system design. 

To gain insights into the number system and apply it to a real-world setup, enrol yourself for the Online BCA course offered by Manipal University Jaipur. The course promotes self-paced learning while facilitating students in hands-on labs.