
Generalized Linear Model – What does it mean?
Have you ever wondered how statisticians or data scientists model outcomes that are not nicely linear, say, counts, binary outcomes, or skewed continuous variables? Or perhaps as you explore analytics and machine learning, you’ve seen “logistic regression,” “Poisson regression,” or “negative binomial models,” and you’ve asked: “What’s the common thread behind them all?”
In a fast-changing job market where employers value people who can wrangle data, draw insights, and build predictive models, mastering these advanced statistical tools can be a differentiator. Upskilling in analytical modeling helps you move beyond dashboards to driving decisions. The concept that unifies many such tools is the generalized linear model (often abbreviated “GLM” or “glm in machine learning”).
In this blog, we will demystify what is a generalized linear model, explore generalized linear model examples, examine when and why they matter, review pros and cons, and finally connect to how Jaro Education’s programs can support your growth in this area.
Table Of Content
Understanding the Core Concepts of the Generalized Linear Model
Learn, Grow, and Excel with Jaro Education
Empower Your Career with Informed Learning Choices
Frequently Asked Questions
Understanding the Core Concepts of the Generalized Linear Model
1. What Is a Generalized Linear Model — Core Concept
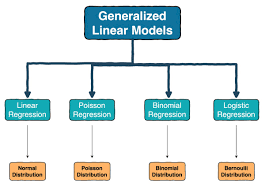
A generalized linear model is a unifying framework that extends ordinary linear regression to accommodate response variables that do not follow a normal (Gaussian) distribution.
Key components:
| Component | Description |
| Random component | Specifies the probability distribution of the response variable (e.g. Binomial, Poisson, Gaussian) |
| Linear predictor | A linear combination of explanatory variables (e.g. β₀ + β₁x₁ + β₂x₂ + …) |
| Link function | A function that links the mean of the distribution to the linear predictor (e.g. log, logit, identity) |
In short:
Response ~ Distribution with mean μ, where g(μ) = linear predictor
Because of this structure, “glm in machine learning” becomes a broad toolset: logistic regression, Poisson regression, gamma regression, etc., all follow the generalized linear model framework.
What makes it “generalized”?
- Not constrained to normally distributed errors
- Ability to model non-negative, discrete, or skewed data
- Flexibility via link functions
2. Generalized Linear Model Examples
Here are some common generalized linear model examples:
- Logistic regression: For binary outcomes (success/failure). Link: logit.
- Poisson regression: For count data (e.g. number of events). Link: log.
- Negative binomial regression: For overdispersed count data (variance > mean).
- Gamma regression: For positive continuous skewed data (e.g. insurance claim sizes).
- Binomial regression (with non-binary counts): For proportions or grouped binary outcomes.
These are all instances of a generalized linear model, differing in distribution and link.
3. When and Why Use a Generalized Linear Model
Consider the following scenario: You work in marketing and want to model how many times a user clicks an ad (a count). Ordinary linear regression is inappropriate (it might predict negative clicks, assume constant variance). Instead, a GLM with a Poisson or negative binomial distribution is more suitable.
When to use a generalized linear model:
- Outcome is binary, count, proportion, or right-skewed continuous
- Variance is not constant across levels of predictors
- The relationship between predictors and the mean outcome is non-linear in raw scale
Why it helps in analytics and machine learning:
- Offers a flexible, interpretable foundation rather than black-box models
- Many “machine learning” classification or regression algorithms build on GLM ideas
- Enables proper modeling of data types common in business, healthcare, finance
4. Pros and Cons of the Generalized Linear Model
| Pros | Cons |
| Interpretability: coefficients have clear meanings on link scale | Requires correct distributional / link assumption |
| Broad applicability across data types | Can be less flexible than non-parametric or ensemble methods |
| Established theory, statistical inference available | Sensitive to outliers or mis-specification |
| Computationally efficient for moderate data sizes | May underperform with extremely complex nonlinear patterns |
It’s important to test model assumptions (goodness of fit, residual diagnostics, overdispersion) before reliance.
5. Industry Demand & Career Relevance
As organizations increasingly rely on data-driven decisioning, professionals who understand core modeling concepts like the generalized linear model gain strategic advantage.
Role vs. Sample Salary (U.S. data)
| Role | Median / Typical Salary* | Notes / Source |
| Data Scientist | ~ USD 112,590 per year | U.S. BLS median for “Data Scientists” in May 2024 |
| Data Analyst | USD 71,000 – 119,000 range (2025 estimate) | Varies by experience and industry |
| Quantitative / Risk Analyst | ~ USD 144,634 (average) | In financial domain |
| Big Data Engineer / Architect | USD 130,000+ | Related advanced data roles |
*These are approximate U.S. market figures. In India, salaries will differ by region, seniority, domain, and employer type.
Key trends & skill gaps for professionals today:
- Many analytics roles expect knowledge of regression and classification modeling
- A gap persists between professionals who know tool syntax (e.g. R, Python) vs. understanding what models do
- Interpretable models (like GLMs) are valued in regulated domains (finance, healthcare)
By mastering what is a generalized linear model, you lay a foundation to build more advanced models (e.g. generalized additive models, hierarchical models, machine learning stacks) in a grounded way.
6. How to Upskill in Generalized Linear Modeling

To build practical skills:
- Hands-on modelling in Python (statsmodels, scikit-learn) or R (glm, MASS)
- Cross-validation, model comparison, regularization (e.g. penalized GLMs)
- Apply to domain datasets: e.g. healthcare claims, marketing click counts, churn prediction
- Understand diagnostics: residual plots, deviance, AIC, overdispersion tests
This is not just an academic topic, these skills are directly useful in business analytics, operations, risk, and more.
Learn, Grow, and Excel with Jaro Education
Program Highlights
- Duration: 10-11 Months
- Format: Live Online Teaching by the Faculty of IIT Madras, Hands-on simulation
- Skills covered: Regression modeling (linear and generalized linear), hypothesis testing, predictive analytics, Python/R programming, model deployment basics
- Ideal learners: Data analysts, business analysts, software/IT professionals transitioning to analytics roles
Jaro also assists with career guidance and counseling support during your course journey. While Jaro does not grant the degree, it ensures you receive mentoring, interview prep, and networking opportunities via the Jaro Connect platform.
Empower Your Career with Informed Learning Choices
In an era where data-driven decisioning is central to business and innovation, mastering tools like the generalized linear model equips you to handle diverse statistical tasks—ranging from classification to modeling counts or skewed outcomes.
You began this blog perhaps wondering: “What’s the common thread behind logistic, Poisson or other models?” Now you see: they all fall under the generalized linear model framework. Understanding this gives you conceptual clarity, interpretability, and a stepping stone into more advanced modeling.
Choosing the right mix of conceptual grounding and practical training is crucial. Jaro Education, with its mentorship, curated programs, and market-aligned curriculum, can guide your next steps. Take charge of your growth: get personalized guidance, apply for the program, and unlock new professional opportunities with solid modeling skills.
Frequently Asked Questions

