
What is Ridge Regression? Definition, Formula, and Examples
When building a predictive model, you might notice something odd, your model performs perfectly on training data but fails miserably on new data. That’s called overfitting, and it’s a common headache in machine learning.
This is where ridge regression steps in. It’s a simple yet powerful technique that keeps your model balanced, not too complex, not too simple, and helps it make accurate predictions on unseen data.
Let’s explore what ridge regression really means, how it works, and why it’s a must-know concept for every data scientist.
Table Of Content
Understanding Ridge Regression
Definition of Ridge Regression
Formula of Ridge Regression
Example of Ridge Regression
How Ridge Regression Works (Step-by-Step)
When Should You Use Ridge Regression?
Ridge Regression vs Other Techniques
Advantages and Disadvantages of Ridge Regression
How to Implement Ridge Regression (Python Example)
Real-World Applications of Ridge Regression
Best Practices for Using Ridge Regression
Common Mistakes to Avoid
Key Takeaways
Conclusion
Frequently Asked Questions
Understanding Ridge Regression
But when you have too many input features or when some of them are closely related (multicollinear), normal regression can give unstable results, the coefficients become large and sensitive to small data changes.
Ridge regression fixes this by adding a small penalty to large coefficients. It doesn’t eliminate them but gently pulls them toward zero. The result?
A simpler, more stable model that performs better on new data.
Definition of Ridge Regression
Ridge regression, also known as L2 regularization, is a modified version of linear regression that adds a penalty term to the cost function. This penalty depends on the square of the coefficients’ magnitude.
By doing this, ridge regression reduces the size of coefficients, preventing any one variable from dominating the model.
In simple terms: Ridge regression helps control model complexity and improves its ability to generalize.
This is why ridge regression in machine learning is widely used when working with large datasets or features that overlap in meaning (for example, “number of rooms” and “house size” when predicting home prices).
Formula of Ridge Regression
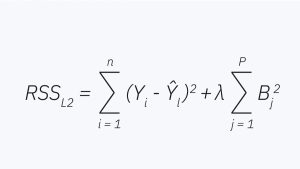
*ibm.com
Here’s the mathematical backbone of ridge regression:
Cost Function=∑i=1n(yi−y^i)2+λ∑j=1pβj2\text{Cost Function} = \sum_{i=1}^n (y_i – \hat{y}_i)^2 + \lambda \sum_{j=1}^p \beta_j^2Cost Function=i=1∑n(yi−y^i)2+λj=1∑pβj2
Where:
- yiy_iyi: actual output
- y^i\hat{y}_iy^i: predicted output
- βj\beta_jβj: model coefficient
- λ\lambdaλ: regularization parameter (controls the strength of penalty)
Think of λ (lambda) as a “tuning knob”:
- If λ = 0 → no regularization (just normal regression)
- If λ is too high → coefficients shrink too much (underfitting)
- With the right λ → balanced, accurate predictions
In short: λ helps you control how much you want to simplify your model.
Example of Ridge Regression
Example 1: Predicting House Prices
Imagine you want to predict house prices based on features like:
- Square footage
- Number of rooms
- Number of bathrooms
- Lot size
Many of these features are correlated, more rooms usually mean larger area. If you use ordinary regression, your model might assign huge importance to one feature and almost ignore the others.
Ridge regression fixes this by shrinking those large coefficients, distributing importance more evenly. This makes your predictions more stable and reliable, especially for new houses not seen before.
Example 2: Text or Image Data
In machine learning, datasets often contain thousands of features, like words in a text or pixels in an image. Ordinary regression would completely overfit here.
But ridge regression helps by penalizing large weights, forcing the model to rely on the most general patterns instead of memorizing details.
That’s why ridge regression in machine learning is used in natural language processing, computer vision, and recommendation systems.
*medium.com
How Ridge Regression Works (Step-by-Step)
- Start with linear regression: Fit the line or plane that minimizes squared errors.
- Add the penalty: For each large coefficient, a cost is added proportional to its square.
- Adjust coefficients: Smaller coefficients mean less variance and more generalization.
- Tune λ (lambda): Control the trade-off between accuracy and simplicity.
- Validate performance: Choose the λ value that performs best on unseen data using cross-validation.
The beauty of ridge regression is that it never eliminates a variable entirely, it just softens its impact. That’s why it’s ideal when every variable contributes something meaningful.
When Should You Use Ridge Regression?
- You have many correlated predictors.
- Your model overfits (too accurate on training, poor on test data).
- You have more features than observations (common in text or genomic data).
- You want to keep all features but make them less extreme.
If your goal is to completely remove unnecessary variables, Lasso Regression (L1 regularization) is better. But if you want a smooth, balanced model, ridge regression is the way to go.
Ridge Regression vs Other Techniques
| Technique | Penalty Type | Effect |
| Linear Regression | None | May overfit or become unstable |
| Ridge Regression | L2 (squared coefficients) | Shrinks coefficients, reduces variance |
| Lasso Regression | L1 (absolute values) | Can shrink some coefficients to zero (feature selection) |
| Elastic Net | L1 + L2 combined | Balances feature selection and shrinkage |
In practice, many data scientists start with ridge regression as a baseline because it’s fast, reliable, and easy to tune.
Advantages and Disadvantages of Ridge Regression
Advantages:
- Prevents overfitting and improves generalization
- Handles multicollinearity, stabilizes models with correlated predictors
- Keeps all variables unlike Lasso, which can remove them
- Simple to implement, works with standard regression libraries like scikit-learn
- Efficient and suitable even for large datasets
Disadvantages:
- Doesn’t perform variable selection (all features remain in the model)
- The penalty makes interpretation of coefficients less intuitive
- Requires tuning λ (regularization strength) for best results
But these are minor trade-offs compared to its benefits, especially for real-world predictive models.
How to Implement Ridge Regression (Python Example)
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Train ridge regression model
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_train, y_train)
# Predict
y_pred = ridge_model.predict(X_test)
# Evaluate
print(“MSE:”, mean_squared_error(y_test, y_pred))
- alpha = λ (lambda): Controls penalty strength
- Use cross-validation to find the best alpha value
- Smaller MSE → better performance
Real-World Applications of Ridge Regression
- Finance: Predicting stock prices using correlated economic indicators.
- Healthcare: Modeling outcomes from hundreds of medical or genetic variables.
- Marketing: Forecasting sales based on multiple campaign parameters.
- Manufacturing: Analyzing machine sensor data for predictive maintenance.
- AI & ML: Regularizing deep learning and linear models to reduce overfitting.
In every case, ridge regression helps create robust and interpretable models.
Best Practices for Using Ridge Regression
- Always standardize your data as features with different scales can distort penalties.
- Use cross-validation to choose the optimal λ.
- Combine with feature engineering for maximum accuracy.
- Compare with Lasso/Elastic Net to understand the trade-offs.
- Visualize coefficient paths, this helps understand how penalty strength affects each variable.
Common Mistakes to Avoid
- Ignoring feature scaling before applying ridge regression
- Setting λ too high (can underfit your model)
- Using ridge when you actually need feature selection
- Misinterpreting shrunken coefficients as unimportant
- Skipping cross-validation during model tuning
Avoiding these mistakes ensures you get a truly balanced model, accurate, simple, and stable.
Key Takeaways
- Ridge regression is a form of linear regression with a penalty on large coefficients.
- It helps prevent overfitting and improves model generalization.
- The λ (lambda) parameter controls how much the model is regularized.
- Use it when features are correlated or when your model performs too well on training data but poorly on test data.
- It’s one of the simplest and most effective tools in a data scientist’s toolkit.
Conclusion
Now that you know what ridge regression is, you can see why it’s a cornerstone of modern machine learning. It’s not just math, it’s a mindset. Ridge regression teaches us that less can be more: smaller coefficients, smarter models, and stronger predictions.
At Jaro Education, we share this same philosophy, empowering professionals to think deeper, learn smarter, and stay future-ready. Our portfolio spans cutting-edge courses across data science, machine learning, technology, and business domains, designed to help you upskill with real-world relevance.
Explore our programs and find the one that best fits your career goals by visiting our official website.
Frequently Asked Questions
Ridge regression is a linear regression technique that adds a penalty to large coefficients to prevent overfitting and improve prediction accuracy.

